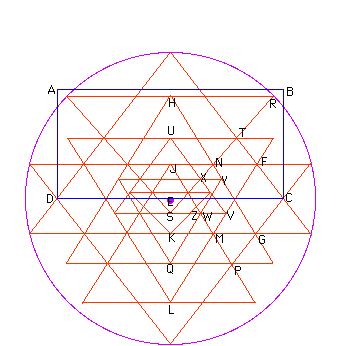
The design was investigated with the largest two triangles having this base angle. The construction continues similar to the 7x7 grid method. The result is striking, for apart from the fact that the error (at Z and W) is not noticeable, the overall shape is very simlar to examples from the literature. The error is only .3616% of length of the diameter. A small change in base angle results in large error - a 53 degree angle has an error of 9.125%!

1. Draw a rectangle of 2 x 1 units (ABCD) for construction of the large pyramid- angled triangles on base DC. The centre of DC is E.
2. Draw the diaganol DB. It's length is sqr-root 5, by Pythagoras.
3. Draw a circle of radius one centered at point B. Extend the diagonal.
4. Bisect the extended diaganol, creating two line segments of length sqr-root 5 plus 1, divided by 2. This length is phi!
5. Mark off the top and bottom vertices of the yantra with compass point at D and length phi, intersecting at a vertical line through E.
6. Draw the circle through these vertices, with compass point at E.
7. Draw in the largest triangles to meet the circle at their vertices. Points F and G are thereby defined. Points H and L are defined by assuming that the dista nces HJ, JK and KL are all equal. Draw LF and extend (an unknown distance). Poin ts M and N are thereby defined.
8. Draw JM down to level with L and complete that triangle. Point P is thereby d efined, and hence point Q after the horizontal is drawn in to meet HNG.
9. The horizontal through H is extended to meet the circle at R. The yantra ther efore touches the circle at eight points. RN is drawn and extended to meet the m id-line, thereby defining S. Point T is also defined, and hence point U after th e horizontal is drawn in to meet LMF.
10. Draw the horizontal at S, meeting LMF at V, and cutting JM at W. Draw W, cutt ing SN at X.
11. Draw the horizontal through X, meeting NG at Y. Draw YQ, cutting SV at Z. The error is represented by the horizontal distance between points W and Z.
12. Draw in the smallest downward pointing triangle, horizontal first.